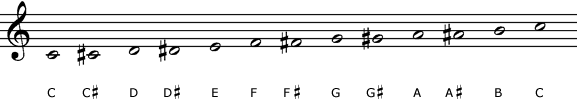Chromatic Pairs is an alternative music notation system by Fernando Terra introduced in October of 2011.
Introduction
Chromatic Pairs is based on the basic five-line chromatic staff. Below is an image of the chromatic scale on a traditional diatonic staff and a basic five-line chromatic staff. (This is just one of many different versions of chromatic staff.)
This basic chromatic staff has great advantages over current traditional notation, as described on the Music Notation Project’s home page. However, the octave spans the full staff (one octave occupies six lines and spaces on the staff), which may make it inadequate if the music has a wide range.
The basic objective of Chromatic Pairs, therefore, was to retain as much of the simplicity of this basic chromatic staff as possible, while allowing more notes to be represented in the same space.
Chromatic Pairs represents two notes on each line and two notes on each space of the staff, doubling the amount of notes represented in the basic chromatic.
A two octave chromatic progression in Chromatic Pairs notation is
shown below:
Notice that, as with a basic chromatic staff, in Chromatic Pairs there
is also no need for key signatures, clefs or accidentals.
Staff, Note Names, and Intervals
Before any further explanation on the notation I would like to suggest that in addition to using a different staff notation system you would consider using a different nomenclature for the notes and different interval naming and notation, because they all share the same characteristic which ultimately makes understanding music much more difficult. This characteristic is that they all have an implicit musical format.
In this sense, the traditional staff notation and note names are worse than the intervals, since they are bound to a very specific format, the C major/A minor key. In this case, even if the music is in a common major or minor key, if it is not in C major/A minor, the music will be poorly represented and unnecessarily difficult. The interval notation should not be as bad, because it is not bound to a specific key, but it is based on the diatonic format, therefore being a bad option if the music departs from that format. Additionally, the interval notation does not profit from using the half-step as a unit, which might be the worst problem of the interval notation (more on this below).
The traditional approach does not take full advantage of equal temperament. Twelve tone equal temperament is the most common tuning today. In this system, the octave is divided equally in twelve half-steps.(1) If you then take the half-step as a unit, you can apply the properties of numbers (like relative position and counting), which are logical and familiar, to notes. This, however, is not easily done using traditional musical tools (the traditional staff, note names and intervals).
That said, we can now come back to the Chromatic Pairs notation that is shown below:

In the picture you see a chromatic progression of pitches starting in ‘Ba’. ‘Ba’ is equal to C in the ‘Bakedi’ note naming system, which I suggest as a better alternative to the alphabetic naming (although one can use the Chromatic Pairs notation with traditional note naming).
Bakedi Nomenclature
Bakedi is a simple nomenclature. I believe most people would be able to memorize it in less than five minutes.
Here is how Bakedi equates to the alphabetical system.
| Ba | Be | Bi | Bo | Ka | Ke | Ki | Ko | Da | De | Di | Do |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | C# | D | D# | E | F | F# | G | G# | A | A# | B |
In addition to being simple, this nomenclature takes full advantage of equal temperament. The purpose of Bakedi is basically to allow FAST INTERVAL CALCULATION and NOTE POSITION establishment. This is possible by means of treating the half-step as a unit and, therefore, profiting from the characteristics of numbers.
In fact, the names were conceived to be NUMBERS.
If I may give an example, imagine a sequence of thirty numbers starting in zero
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
Now imagine that we don’t use the decimal system, which is based on groups of ten numbers, but a system based on groups of four numbers, as such
| 0 | 1 | 2 | 3 |
| 10 | 11 | 12 | 13 |
| 20 | 21 | 22 | 23 |
Bakedi uses the letters ‘aeio’ to be the names and symbols of the “numbers” ‘0123’
| a | e | i | o |
|---|---|---|---|
| 0 | 1 | 2 | 3 |
and consonants ‘B K D’ to correspond respectively to 0, 1 and 2, as the “tens” of the numbers. This is illustrated in the table below;
| 0 | 1 | 2 | 3 | ||
| a | e | i | o | ||
| 0 | B | Ba | Be | Bi | Bo |
| 1 | K | Ka | Ke | Ki | Ko |
| 2 | D | Da | De | Di | Do |
In this way I have 12 notes Ba Be Bi Bo Ka Ke Ki Ko Da De Di Do, which are divided equally in three sets of four notes.
The sequence of vowels (aeio) is popularly known, and known in that specific order (from a to o), since children are educated that way while learning to read. I believe this note naming gives a good idea to the musician of the notes positions in relation to each other, and that could allow for the musician not to depart as much from the notes in ABSOLUTE terms (the actual note names), when they need to think in RELATIVE terms (i.e. intervals).
Intervals
Regarding intervals I just use the names of the numbers, i.e. if a note is four half-steps apart, then their interval is four. Here is how this system equates to the traditional system:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| unison | Minor 2nd | Major 2nd | Minor 3rd | Major 3rd | Perfect 4th | Dim 5th | Perfect 5th | Minor 6th | Major 6th | Minor 7th | Major 7th |
Beyond the octave a possibility is to use the letter – o – for octave, and proceed as o+1, o+2, o+3, … or o1, o2, o3, …
Chromatic Pairs Features
I would now like to talk about some of the characteristics of the CHROMATIC PAIRS notation. Here is the Chromatic Pairs notation again:

In Chromatic Pairs a chromatic progression occurs as successive changes in color and upward jumps as shown above.
Although this is a bit more complex than the basic chromatic staff (shown below),

image source: musicnotation.org
Chromatic Pairs is favored by some nice properties. It is organized in PAIRS of BLACK and WHITE and counting in pairs (0,2,4,6,8,10) is almost as easy as counting units. It is also organized in GROUPS OF FOUR HALF-STEPS from one line to the next, as explained below:
In every staff there are four types of notes:
- Black notes on lines (notes ending in a, Ba Ka Da)
- White notes on lines (notes ending in e, Be Ke De)
- Black notes on spaces (notes ending in i, Bi Ki Di)
- White notes on spaces (notes ending in o, Bo Ko Do)
(You can notice how these four types of notes relate conveniently to Bakedi.)
Therefore, the interval of four half-steps is very easily recognizable. To jump to a note four half-steps apart just go to the next note of the same kind. By doing that, you will also arrive in a note ending in the same vowel in Bakedi.
It is essential for a notation to be logical, so you can follow some simple steps to conclude what is the interval between two given notes, while learning the notation. However, the idea is that, with some practice, you could abandon those steps and just instantly recognize any interval.
Relating Chromatic Pairs to Bakedi
As said earlier for each type of note representation in the staff, there is a vowel.
- Black notes on lines (notes ending in a, Ba Ka Da)
- White notes on lines (notes ending in e, Be Ke De)
- Black notes on spaces (notes ending in i, Bi Ki Di)
- White notes on spaces (notes ending in o, Bo Ko Do)
You can also notice every BLACK NOTE ends either with ‘A’ or ‘I’, every WHITE NOTE ends either with ‘E’ or ‘O’.
Besides that, every consonant represents a line and a space (the space immediately above it) on each octave, as shown in the image below, and this also represents a PROGRESSION IN 4 HALF-STEP INTERVALS.
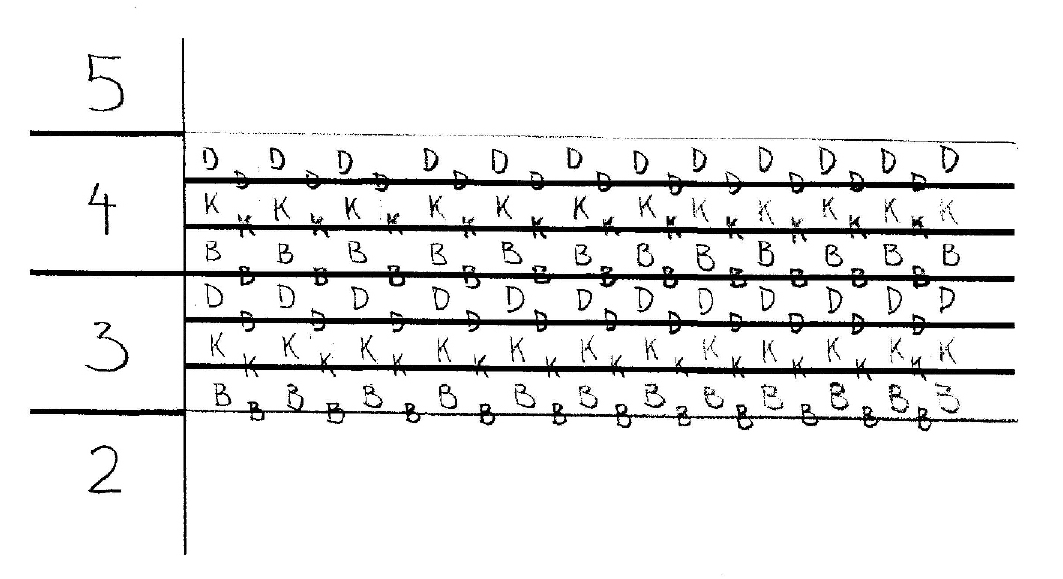
The Octaves Display
To the LEFT OF THE STAFF you can see numbers that show the OCTAVES which encompasses the notes shown at their right in the staff.

So, for instance ‘Ba4’ to ‘Do4’ have to their left the number four, above ‘Do4’ the next note is ‘Ba5’ and this is represented in the left as the beginning of the fifth octave.
In the ledger line region there are two octaves that use the same space (as in traditional notation). From bottom to top, in our example above, the fourth octave is represented by a 4 with an arrow upwards coming from the third octave. From top to bottom there is a similar indication of the third octave coming from the fourth.
These octaves numbers are assignable and should be determined according to the musician’s necessity.
Rhythm
Chromatic Pairs borrows the rhythm of the traditional notation almost entirely, but since there is a conflict with the half-note and quarter-note because of the use of color to determine pitch, the half-note is changed to the form shown in the image below:
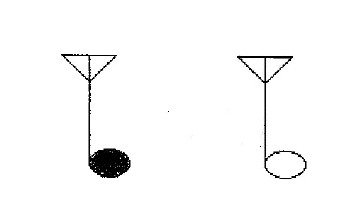
An explanation on the rhythm of notations that use color to indicate pitch is given in this tutorial.
Conclusion
The traditional musical staff notation and traditional nomenclature, both of intervals and notes, is overly complex and do not represent the music well. This is due to the fact that they have an intrinsic musical format.
This problem seems worst for the note nomenclature and traditional staff, since they are bound to a very specific format, the C major/A minor key. This bond inflicts a lot of unnecessary effort on the musician, who has work around this format.
Additionally, the traditional system doesn’t benefit enough from the properties of numbers, which can be used when you consider the half-step to be a unit.
Chromatic Pairs combined with the Bakedi nomenclature and different names for intervals were proposed as alternatives to the traditional system. This new system has the objective to be as simple as possible and to allow for the use of the half-step as unit, therefore permitting fast note positioning establishing and interval calculation.
The ultimate purpose of the system is to make learning, reading, writing and understanding music easier.
Note on Equiton: Although Chromatic Pairs was conceived based on the basic chromatic notation alone and without previous knowledge of similar notations, there is a notation which is similar to Chromatic Pairs in regard to pitch, but that makes further modifications to the traditional notation. The name of this notation is Equiton, and it was designed by Rodney Fawcett in 1958. In this page you will find a description of Rodney Fawcett’s notation along with a link to a page that describes his work (although it is a very bad translation), and a pdf file of Mark Gould’s work, that further develops on Equiton.
(1) This is a crude definition of twelve tone equal temperament, but fits the purpose of a quick explanation. On the following link the term is better defined http://en.wikipedia.org/wiki/Equal_temperament