Intervals are one of the essential elements of music, the building-blocks that make up its structures. Melodies, scales, and chords are all patterns of melodic or harmonic intervals, and the notes in any given key belong to that key because of their interval relationships. Playing by ear and improvising involve hearing and playing music by interval relationships, and intervals are indispensable for understanding music theory.

Because intervals are so important, the way they are represented in music notation is particularly significant. It is surprising how limited, indirect, and inconsistent the representation of intervals is in traditional notation. In the next tutorial we explore how alternative notation systems can portray interval relationships with much greater clarity and accuracy. How might a better notation system improve awareness of interval relationships and the ability to understand and play music?

Note that while most of the illustrations below show harmonic intervals, this discussion applies equally to melodic and harmonic intervals.

Intervals on the Traditional Diatonic Staff

At first glance traditional notation seems to represent interval relationships consistently. Some intervals are always one line-note and one space-note. Others are always two line-notes or two space-notes. This consistent pattern makes it easy to distinguish different intervals at a glance. Each interval always has its own particular appearance or “look” regardless of the key signature, clef, or accidental signs.

Despite this consistency, things are not as simple as they may appear. While it is easy to identify an interval’s name (2nd, 3rd, 4th, etc.), it is impossible to tell from the vertical distance between the notes on the staff what an interval’s quality is (major, minor, perfect, augmented, diminished), or exactly how many semitones it spans. Many intervals that appear to be the same actually sound different and are played differently. For example, two thirds may look the same, but one may be a major third and the other a minor third.

Take a moment to look at the diagram below and try to fully identify the intervals.

• Which 2nds, 3rds, 6ths, 7ths, and Triads are major and which are minor?
• Are the 4ths and 5ths all perfect, or are some augmented or diminished?
• How would a different clef sign or key signature change things?

Diatonic Intervals in Traditional Notation
Intervals that appear the same may be different, depending on staff position, key signature, and clef. Click the buttons below to see how different clefs and key signatures change the identity of the intervals, while their appearance on the staff remains the same.

No Clef or
Key Signature
Treble Clef
C Major, A Minor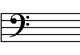
Bass Clef
C Major, A Minor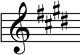
Treble Clef
E Major, C# Minor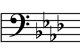
Bass Clef
Ab Major, F Minor

Numbers = semitones spanned by the interval. Maj = major. Min = minor. Perf = perfect. Aug = augmented. Dim = diminished.

By itself an interval’s appearance is ambiguous and does not provide enough information to identify the interval. To play an interval one must first take into account:

• its position on the staff
• the clef sign
• the key signature
• any accidental signs

With all these factors in mind, one must go through the mental procedure of calculating the identity of the individual notes (ie: “C sharp and G natural”) which finally reveals their interval relationship. In other words, to play an interval requires already knowing the pitches of its notes. This affects the way in which music is read and played.

This fundamental ambiguity and inconsistency in the appearance of intervals makes it much more difficult to play by reading the interval relationships between the notes. Because reading by intervals depends upon knowing the pitches of the notes, it is simpler to just play the notes by their pitches. This has implications for learning to improvise or play by ear — skills that largely entail playing by interval relationships rather than playing by the individual pitches of notes.

Even in the simplest case of C major with no accidental signs, intervals are not clearly or directly represented in traditional notation. What one sees does not fully correspond with what one plays or hears. This frustrates and undermines a musician’s understanding and proficiency with the patterns of intervals found in diatonic music or any given style or genre of music. Consider how important basic intervals are obscured: whole steps and half steps which are the basic elements of diatonic scales and modes, and major and minor thirds which are the fundamental building blocks of diatonic chord structures.

How might the aspiring musician’s understanding of music and proficiency with common interval patterns improve if interval relationships were represented clearly and were not obscured and hidden from view? How might the basic understanding of harmony and music theory improve if the appearance of interval relationships was clear and consistent?

Intervals and Accidental Signs

We have mostly been considering how the inconsistent pitch axis of the traditional diatonic staff has a distorting effect on the accurate representation of interval relationships. Now we will consider how accidental signs (and by extension key signatures) also distort this pitch axis and add another layer of complexity to reading the interval relationships between notes.

The following illustration shows how an interval containing the same two staff degrees (C and D, a second) can actually have many different meanings in traditional notation, depending on the key signature and accidental signs.

Accidental signs allow for twenty-five possible variations of any given interval
Numbers = size of the interval in semitones. Roll your cursor over the image to see the more likely variations.[1]

Although some of these twenty-five examples are largely theoretical and would be very improbable in actual music, there are still quite a few realistic cases.[1] There is a complex one-to-many mapping between (1) the vertical distance between two notes on the staff and (2) the many possible sizes of the interval that is played and heard. In other words, the visual representation is not proportional to the sound it is representing. What one sees does not correspond to what one plays or hears. In technical terms, the pitch axis in traditional notation is highly nonlinear.

By contrast, on a chromatic staff, intervals are always unambiguous, being shown directly by the vertical distance between two notes, which is exactly proportional to the actual size of the interval as it is played and heard. In technical terms, the pitch axis on a chromatic staff is linear.[2] (Recall that on a chromatic staff key signatures and accidental signs are not required.)

On a chromatic staff there is just one possible meaning for any given interval
Each interval has one distinct appearance that always spans the same number of semitones. In this case, one semitone.

In the tutorial on Intervals in 6-6 Music Notation Systems we will explore how alternative notation systems with a chromatic staff improve upon traditional notation when it comes to representing interval relationships.

But before moving on, one last illustration further demonstrates how the appearance of intervals, the vertical distance between the notes, may not correspond with how they sound, the number of semitones they span. (Intervals that have the same number of semitones are known as enharmonic equivalents.)

In traditional notation intervals that sound the same may look different and vice-versa

Intervals grouped by sound (semitones):

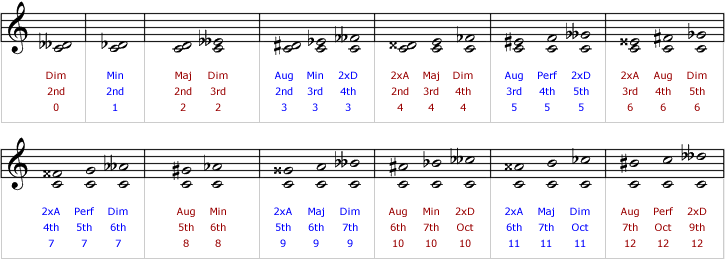
Intervals grouped by appearance (names):

Numbers = Semitones spanned by each interval, Maj = major, Min = minor, Perf = perfect, Aug = augmented, Dim = diminished, 2xA = doubly augmented, 2xD = doubly diminished.

How can alternative notations that use a chromatic staff and a 6-6 pitch pattern improve upon these ambiguities and inconsistencies in the representation of interval relationships in traditional notation? Check out Intervals in 6-6 Music Notation Systems to find out.