TwinNote Music Notation by Paul Morris was designed in December of 2009 when it was first introduced on this wiki page. For more complete documentation of TwinNote, see the TwinNote Music Notation website and also this page on the Music Notation Project’s website.
TwinNote was inspired and influenced by Twinline notation in its various versions by de Vries, Reed, and Keislar (as well as Bilinear notation by Sotorrio). When compared to Black-Oval Twinline (Morris’ version of Twinline and previous notation system of choice), TwinNote is simpler, using two note shapes, triangles pointing either up or down. The two orientations of the triangles highlight the 6-6 pitch pattern. In one whole tone scale all the triangles point upwards, and in the other they all point downwards. In a chromatic scale there is a regularly alternating pattern of triangles pointing upward and downward. This way of representing a 6-6 pitch pattern gives intervals a more clear and consistent appearance (than is found in Black-Oval Twinline notation, for example).
Below is a chromatic scale with alternating solid and hollow noteheads. This was the original note layout, but it is no longer accurate. In March 2011 Morris shifted the notes up a semitone so that the notes C D E F G A B would correspond to the lines and spaces of the traditional treble clef staff. The images below show the previous note assignments (with only C D E corresponding with the treble staff).
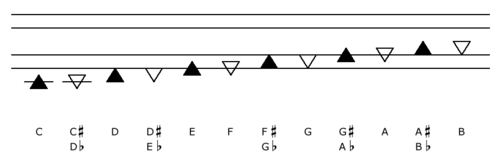
Chromatic scale with original note layout (no longer accurate).
Interval Profile
Below is an llustration showing TwinNote’s complete “interval profile.” You can see that the intervals in this system have a more consistent appearance compared to intervals in Black-Oval Twinline. (See also this discussion of influences on TwinNote.)

Pitch-Proportionality
Below is an illustration showing how TwinNote is “pitch-proportional,” having a proportional vertical pitch axis:
The distance between the centers of any two noteheads is always proportional to the musical interval between them. See the MNP’s 8th criterion for alternative notation systems: “The notation possesses a fully proportional pitch coordinate, where each of the twelve common pitches is spaced in a graphic manner, so that progressively larger pitch intervals have progressively larger spacing on the coordinate, providing a visual representation of each interval that is exactly proportional to its actual sound.”
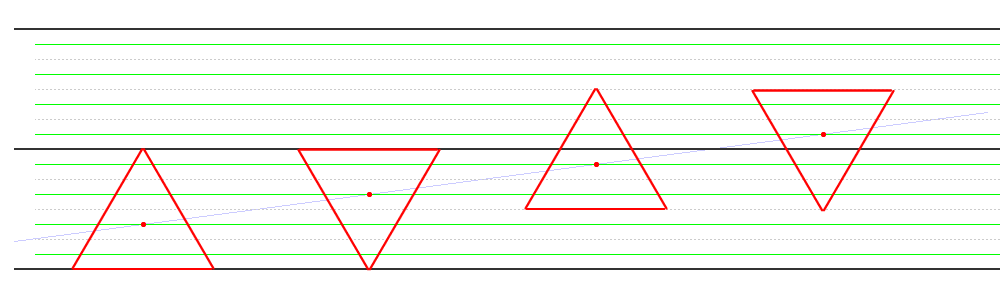
In the image above the centers of the triangles are shown at 3/8 of the triangle’s height (the distance from its base to its tip). In geometry there are various kinds of centers for any given triangle, for example: Incenter, Circumcenter, Centroid, and Orthocenter. The most relevant center in this case is arguably the centroid, also known as the triangle’s “center of gravity”.
For an isosceles triangle like the ones used in TwinNote, the centroid is located at 1/3 (0.333…) of the triangle’s height. (Interestingly enough, changing the width of an isosceles triangle does not affect the centroid’s position on the vertical axis.) 1/3 of the height is only slightly less than the 3/8 (0.375) shown in the image above.
To find the difference: 0.375 minus 0.333… equals 0.041666… of the height of the triangle. The triangle’s height is the same as the distance between two staff lines which are commonly spaced about 1/16 (0.0625) of an inch apart. So 0.0416 times 0.0625 is only 0.0026 of an inch in terms of actual real-world difference between the centroid and the 3/8 point.
This is so miniscule that it is effectively negligible, and could be easily negated by small adjustments in musical fontography and engraving. Consider also that the notes as perceived on the page are not pure, ideal, abstract geometric objects, and are subject to the vicissitudes of human perception. (How does the line thickness of hollow notes affect the perception of their center? How does the thickness of the staff lines come into play? Is the base of the triangle the top or bottom edge of the staff line it rests on? How important are the positions of the top and bottom edges/points of two triangles relative to each other, as compared with their centers, when determining relative vertical position?)
The following image illustrates the difference between the centroid at 1/3 and the 3/8 point used in the image above. Even at this large magnification, the difference is quite small.
