Some musicians may object to alternative music notation systems that use a chromatic staff because of their (presumed) omission of the traditional distinction between enharmonically equivalent notes (like C# and Db). This tutorial looks at the reasoning behind this objection, considers several ways it can be addressed, and ultimately shows it to be unfounded. This is an obscure and often complex topic, and some background knowledge about enharmonic equivalents, tuning systems and practice, and diatonic function may be helpful.

Enharmonic Equivalents in Traditional Notation and on Chromatic Staves

In western music theory and practice, notes such as C# and Db are understood to be “enharmonically equivalent.” If you include double sharps and double flats, there are three of these notes for all but one of the twelve degrees of the chromatic scale:

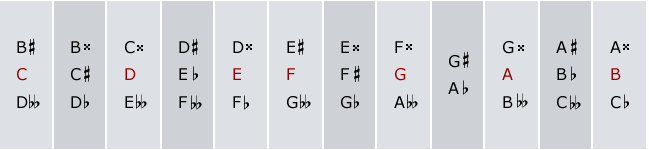
These enharmonically equivalent notes:

• have different names and
• are represented differently in traditional notation

And yet they:

• sound the same since they have the same pitch(or very similar pitches, see below) and
• are played the same way on most instruments

This is another example of inconsistency in traditional notation’s representation of pitch. Notes that sound the same may appear on different lines or spaces. The traditional diatonic staff already has an irregular pitch axis, and the use of accidental signs makes the relationship between pitches less consistent and more obscure. (See our tutorial on Intervals in Traditional Music Notation.)

Enharmonic Equivalents in Traditional Notation

Notes that sound the same and are played the same appear at different vertical positions on the staff.

With only sharps, flats, and naturals: (7 diatonic notes) x (3 variants) = 21 notes per octave:

And again including double sharps and double flats: (7 diatonic notes) x (5 variants) = 35 notes per octave:

Chromatic staves are more consistent than the traditional diatonic staff in representing the relationships between pitches. Notes that are enharmonically equivalent share the same position on a chromatic staff. Notes that are played the same, and sound the same, also look the same.

Below is an illustration of what these notes might look like on a basic five-line chromatic staff. (We are using this five-line chromatic staff just to illustrate the principle, not to suggest that it is preferable to other types of chromatic staff.)

Enharmonic Equivalents on a Generic 5-Line Chromatic Staff

Notes that generally sound the same and are played the same share the same vertical position on the staff. (Shown without any alternative accidental signs, see below.)

With only sharps, flats, and naturals: (7 diatonic notes) x (3 variants) = 21 notes per octave:

And again including double sharps and double flats: (7 diatonic notes) x (5 variants) = 35 notes per octave:

This raises a series of questions that we address in the remainder of this tutorial:

• Is there a need to differentiate between enharmonic equivalents? What are the reasons for doing so? How compelling are they?
• Can one have the advantages of a chromatic staff and still differentiate between them?
• What kinds of symbol systems would best allow for differentiating between these notes on a chromatic staff, if this was desired?

The Case for Distinguishing Between Enharmonic Equivalents

The argument for visually distinguishing between enharmonically equivalent notes asserts that they are not completely equivalent or interchangeable. In this view, important musical information would be lost if notes like C# and Db were notated in the same way, collapsing the distinction between them. Twelve notes per octave are not enough; twenty-one notes per octave are needed, or even thirty-five with double sharps and flats. Whether one agrees or not, it is important to understand this argument, and what is at stake in it.

There are two related reasons why distinguishing between these notes may be desirable:

1. Intonation

In the twelve-tone equal temperament tuning system, enharmonic equivalents have the same pitch. This is by far the most common tuning system in use in western music today, and has been since the romantic period of the early 1800s. In most other historical tuning systems, which are now rarely used, and in some microtonal scales used by experimental musicians, these notes have slightly different pitches (and cease to be “enharmonically equivalent”).[1] For advanced musicians using one of these uncommon tuning systems, or making slight deviations in pitch for expressive purposes, a visual distinction between these notes is one of several factors that help them fine-tune their intonation. Of course, this assumes they are either singing, or playing a flexible-pitch instrument like a violin or trombone that can make these minute adjustments in pitch. Some uncommon fixed-pitch instruments also provide different pitches for these notes by having more than twelve notes per octave. For example: microtonal keyboards or historical keyboards with split keys.

2. Harmonic and Melodic Function

In traditional western music theory and composition there are conventions about the function of notes based on their position within the prevailing key. These conventions involve using different enharmonic equivalents in order to communicate different types of relationships between notes. For example, in a melody ascending chromatically from F to G, the intermediate note is typically spelled as an F# rather than a Gb. The opposite would be true if the passage was descending chromatically from G to F. [2] In terms of harmony, the interval between C and E is a major third, while the interval between C and Fb is a diminished fourth. Different intervals such as these convey different meanings about their function in a musical passage, even if they sound exactly the same in twelve-tone-equal-temperament (since E and Fb would have the same pitch). This information about the function of particular notes and their relation to other notes may be useful to advanced musicians and composers as they interpret or compose music.

An Example

An example will help to illustrate these two different aspects. In the two passages on the right, the second chords (F# A# E and Gb Bb E) are enharmonically equivalent. They are played identically in both cases, if you are using equal temperament, but their harmonic functions are different. In the first example, the chord functions as a dominant seventh (V7) in the key of B, whereas in the second it functions as an augmented sixth triad (Aug6) in the key of Bb.[3] The spellings of these two chords are different, not just because they are in different keys, but also because they have different harmonic functions.

If not playing in strict equal temperament, the two chords in question could also have different intonation. For example, the G flat in the second passage might be played slightly lower (flatter) than the F sharp in the first passage, to accentuate the “desire” of the Gb to resolve downward to F in the second case. That would be an example of enharmonic equivalents being tuned differently.

However, for the same reason, the E in the second example might be tuned slightly higher (sharper) than the E in the first example, to accentuate its resolution upward to F. Notice that these two E notes have the same spelling in both examples (although only one requires a natural sign). This demonstrates that such adjustments in intonation are not limited to notes that are spelled differently (i.e., enharmonic equivalents), and often they are not directly indicated by traditional notation at all.

In general, intonation is less a matter of following explicit cues given in the notation, and more a matter of playing in tune, and making subtle adjustments by ear, based on a note’s melodic or harmonic relationship to other notes. The particular spelling of a note is just one of several factors that might affect a note’s intonation. A skilled musician performing at a level where enharmonic equivalents are played with slightly different intonations will most likely be making other intonational adjustments that are just as significant, and will be making them by ear without any direct cues from traditional notation.[4]

Various Approaches

There are at least three different approaches to the representation of enharmonic equivalents in chromatic staff notation systems:

1. Not Explicitly Differentiating Between Enharmonic Equivalents
   …while assuming twelve-tone equal temperament for intonation and/or relying on contextual cues and conventions for harmonic/melodic function and intonation.
2. Using an Alternative Accidental Symbol System
   …to provide the same information that is given by accidental signs in traditional notation.
3. Using a More Comprehensive Microtonal Symbol System
   …to specify intonation more precisely than is possible with standard accidentals,
   as well as more consistently across different tuning systems and microtonal scales.

These approaches involve nomenclature as well, since the traditional note and interval names make a distinction between enharmonic equivalents. For example, the first approach above lends itself to using a novel nomenclature for notes and intervals, otherwise the names of some notes and intervals would remain ambiguous.

To conclude, there are different views on just how important it is to distinguish between enharmonic equivalents in music notation, and on how not doing so might affect the understanding of their intonation and tonal function. Fortunately, there are also corresponding approaches to representing them (or not) in a chromatic staff notation system.

Intonation and tuning systems are complex topics that go beyond the scope of this tutorial. For further reading, see Atlas of Tonespace from the Intuitive Instruments for Improvisors website. Other articles include Intonation by professor Julie Stone, and Tuning & Intonation by Joseph Butkevicius. The Huygens-Fokker Foundation maintains a massive bibliography on tuning, including many links to online source material.