Elsewhere on the Music Notation Project’s Web site, we focus on systems that represent the chromatic scale graphically, with a pitch-proportional staff. However, it is instructive to also examine systems that represent the chromatic scale numerically and not necessarily graphically. In such systems, pitches are represented by numerals.

One benefit of a numerical approach is that it makes it easier to calculate the interval relationships between notes — instead of, or in addition to, representing interval relationships graphically on a staff. Most of these systems place all the notes/numbers of one octave at the same vertical position. This approach allows these systems to be vertically very compact. However, this benefit is gained by sacrificing the benefits of a pitch-proportional graphical representation of notes (#8 of our Desirable Criteria…).

This tutorial contains two parts: a historical background written mostly by Dominique Waller (himself an inventor of a numerical notation system), and a chronology of important innovations, extracted from information in Gardner Read’s Source Book of Proposed Music Notation Reforms.

Also see the overview of nomenclatures page on the Music Notation Project Wiki, especially Dominique Waller’s document on the various single-digit symbols that have been proposed as substitutes for double-digit numbers in numerical notation systems (i.e. 10 and 11).

Historical Background

(with many thanks to Dominique Waller)

In considering the development of numerical musical notation through the centuries, one can see that there has been a general progression in the use of numbers by notation inventors as everyone’s understanding of arithmetic itself progressed.

Europeans generally used Roman numerals until the mid-16th century, when Arabic numerals became widely adopted. Even after the adoption of Arabic numerals, the zero (which is so useful for measurement) was often ignored, or at least not fully understood as a legitimate number. Roman numerals, which are seen on many sundials and clocks to this day, were still sufficient for counting and ordering things. One can speculate that it took some time for Europeans to become fully acclimated to the idea of considering numbers as direct representations for measurement, as opposed to names for positions in a sequence. Thus the early numerical systems didn’t measure intervallic distances directly, but simply named the successive degrees of the diatonic (modal) scale. Since these successive degrees are unequally spaced (with some the distance of a semitone apart and others a whole tone), the concept of using pitch names for direct measurement of musical intervals didn’t apply.

Here is an early example written in a Spanish tablature for the harp:
 

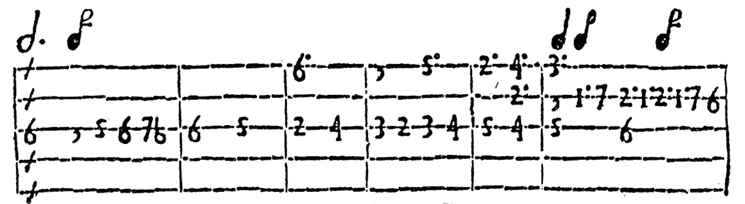
This figure comes from Hernando de Cabezón, Obras para tecla, arpa y vihuela, Madrid, 1578.The piece is written in the idiom of Renaissance polyphony, here with five different voices. Lines represent individual voices, numbers denote the seven degrees of the diatonic scale, and various diacritical signs (dots, commas) indicate different octaves.

The harmony was fundamentally unaffected by this coding, as it is itself based on those seven steps, beginning with the name of the intervals themselves: unison, second, third, fourth etc. Those intervals are variable, as they can be minor, major, augmented, diminished, etc., depending on the scale itself and the alterations (simple or, later, double) assigned to the notes. Therefore, this coding was just the numerical translation of a 7-tone scale and of the harmony that goes with it.

The following figure (from Traité de la musique théorique et pratique contenant les préceptes de la composition, 1639, new edition 1646, p. 77) shows what is perhaps the first numerical staff in history, designed by Jesuit father Antoine Parran:
 

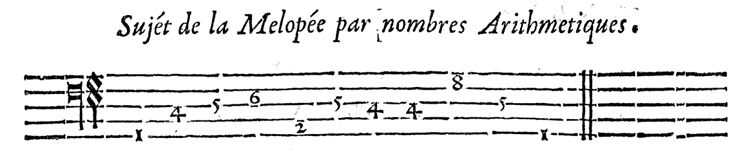
On this staff, the subject (theme) of the composition is given in the form of diatonic numbers, in place of noteheads.

Here is an example of Jean-Jacques Rousseau’s numerical notation (from Dictionnaire de l’Encyclopédie de d’Alembert et Diderot (published 1751–72), Volume VII, pl. IV, fig. 17):
 

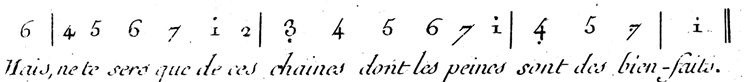
The dots indicate a shift to an upper or lower octave.

As the result of the general acceptance of the positional system of numerals, that is, the place-value notation using Arabic figures and including the zero, it became possible to easily subdivide numbers on a decimal basis, a fact that allowed numbers to develop the new function of measuring things with precision. In the 16th century, the mathematician Simon Stevin advocated for a duodecimal (that is, base-12) number system. The Western world did not follow him. However, in addition, he advocated for fractional division after the decimal point, and this time he opened the way for the uses of decimal divisions in unit systems. Later on, new standards of rational measurement were invented that took advantage of these advances, resulting in the adoption of the metric system by the French Convention in 1792.

In the course of the 18th century, equal temperament began to settle down in the mind of musicians and music theorists. As a consequence, notation systems with the 1-12 series then flourished, but this nomenclature could still be understood as ordinal numbers ordering and naming the notes of the series. With the next stage, the 0-11 series, it became self-evident that numbers endorsed the new function of measuring pitches and intervals with the prony (twelfth part of the octave) as the unit of measure, exactly as a tape measure does.

As early as 1832, Baron Blein, a French engineer, realized that this could provide the basis for a new language for harmony, and he began to develop chord analysis in this pure arithmetical coding together with a chromatic nomenclature of 12 syllables. But he didn’t have the idea of using those same numbers in his 7-line staff system, which was plainly chromatic. (That’s why he is not registered in Gardner Read’s book as a numerical system inventor; see p. 17.) The following figure by baron Blein (from Principes de mélodie et d’harmonie, Paris, 1838, p. 93, French National Library) shows a two-octave chromatic scale on a chromatic staff. The numbers underneath measure intervals in terms of semitones.
 

In the late 19th century, inventors such as the Austro-Hungarian Leo Kuncze and the Mexican Julián Carrillo (see chronology below) introduced numerical notation systems based on the chromatic scale. Kuncze’s system used the series 1-12, whereas Carrillo’s used 0-11. Here are the four main octaves in Kuncze’s notation, written in between the treble and bass staves of traditional notation:
 

Both Kuncze and Carrillo understood that if the horizontal bar is to symbolize the octave, then it is useful to have it above ciphers for low octaves and under ciphers for high octaves. Whereas other inventors had followed a logical impulse to place a symbol above a number to raise its octave, and below it to lower its octave, Kuncze and Carrillo recognized that the opposite scheme has the advantage of resulting in a vertical pitch axis of a sort: higher octaves appear higher on the page than lower octaves. The resolution of this pitch axis is only one octave, whereas the pitch-proportional chromatic notations described elsewhere on this site have a pitch resolution of one semitone. (In traditional notation, the resolution of the pitch axis is irregular, being either a semitone or a whole tone and, in the presence of accidentals, sometimes becoming an augmented second, etc.)

Here are eight octaves in Carrillo’s system (from Nueva escritura musical, 1895), placed below traditional notation as a reference:
 

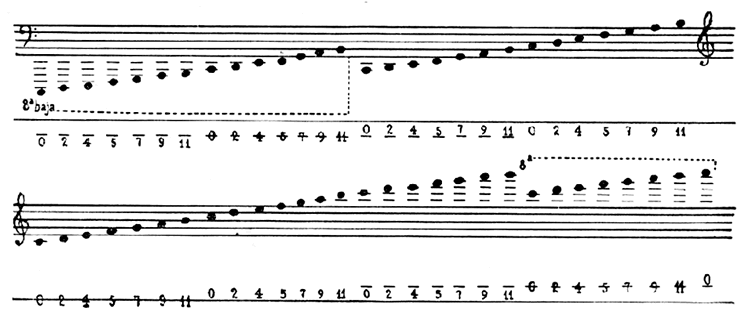
For maximum compactness, Carrillo places numerals on, under, over and between line or bars.

Many other inventors have introduced alternative symbols for the numbers 10 and 11, to facilitate duodecimal (base-12) calculations and to avoid ambiguity when notes are placed close together. (For example, is 11 a single note or two instances of pitch 1 in close rhythmic proximity?) See the discussion of such symbols on the Music Notation Project’s Wiki.

Today, a diatonic numerical notation using the numbers 1-7 is widespread in China, where the system is known as jiǎnpǔ, literally “simplified notation” (see the jiǎnpǔ Wikipedia article). The digit 0 represents a rest.

The seven notes are apparently not necessarily identical to those of the European major scale, according to the Gongche notation article on Wikipedia. Much traditional Chinese music is based on pentatonic scales, and yet the Chinese have apparently adapted to a 7-degree notation. One might be encouraged by this fact to speculate that it should therefore be similarly possible for a 12-degree notation to take hold in the West, even though most Western music is firmly grounded in the diatonic scale.

Chronology of Innovations in Numerical Notation

Gardner Read’s Source Book of Proposed Music Notation Reforms (Greenwood Press, 1987) describes many alternative notation systems. Chapter 5, “Numerical Systems,” describes 44 music notation proposals in which pitches are represented by numbers (at least supplementarily, if not exclusively). The following list summarizes that chapter, focusing only on the first historical appearance of specific features.[1]

Before 1877

1560: the earliest numerical system appears, by Pierre Davantès. It and all other systems until the year 1877 use the numbers 1-7 to indicate one octave’s worth of modal or diatonic pitches. The intervening chromatic pitches are either ignored or represented by various alterations of these numbers. Generally ut or C is 1. (In the early modal systems, ut is G, represented by 1.)

1877 – 1900

1877: the first chromatic numerical system appears, by H. Hohmann. It uses 1-9 for C through Ab, a sort of cross symbol for A, 0 for Bb, and B for B (the English B, not the German B). Other diatonic-based numerical systems (using the numbers 1-7) continue to appear in the 19th and 20th centuries.

1877: Leo Kuncze uses 1-9 for C-Ab, 0 for A, and upside-down 1 and 2 for Bb and B respectively. (See the image above.)

1892: Hans Schmitt uses 1-9 for C-Ab, a small circle with “horns” for A, U for Bb, and S for B.

1895: the first zero-based system appears, by Julián Carrillo, with 0-9 for C-A, followed by 10 and 11 for Bb and B. (His notation system can be seen above and is documented at the official Web site of the Julián Carrillo Estate: 123.)

1897: Charles Guilford uses 1-9 for C-Ab, followed by 10, 11, 12 for A, Bb, B.

1900 – 1987

[not mentioned in Read’s book] 1946 or earlier: Carl-Gustaf Rosengren’s system appears to place notes at three vertical positions per octave.

1966: John Robbins introduces a highly idiosyncratic system in which the notes use a different number sequence for left versus right hand of the piano, and there are only 10 unique digits for 12 unique pitches.

1970: Christopher Crocker’s system uses 1-12 for do through ti.

1973: Yael Bukspan proposes a system that uses binary numbers for the 12 chromatic pitches (though not the series of binary numbers one might expect).

1983: Robert Stuckey introduces the first system that uses numerical noteheads on a pitch-proportional chromatic staff. It uses 0-9 for C-A, followed by X and N for Bb and B. The other chromatic numerical systems to this point typically placed all the numbers of one octave at the same vertical position. Stuckey’s system is presented on our site.

1987 – Present

The following systems were proposed after Read’s book was published in 1987. There are likely others that have escaped our attention.

FinKeys Notation System by Victor Mataele uses the numbers 1-9 followed by the letters X, Y, and Z (C is 1 and B is Z).

Hamburg Music Notation by Robert Elisabeth Key, uses 0-9 followed by the letters A and B (C is 1, A is A, Bb is B, and B is 0). Note that “Robert Elisabeth Key” is a pseudonym.

Numbered Notes by Jason MacCoy uses 1-12 for C-B, and uses a pitch-proportional chromatic staff with lines spaced a minor third apart.